1. 支持向量机是什么?
支持向量机(Support Vector Machine,简称SVM)是机器学习领域中的一种经典算法。它广泛应用于分类和回归任务,尤其在分类问题中表现突出。本文将用通俗易懂的语言,带你全面了解支持向量机的核心概念、工作原理、优势以及应用场景。
支持向量机可以看作是一种“聪明的线”或“聪明的平面”,它的任务是根据已有数据划分空间,确保能够尽可能准确地区分不同类别的数据。例如,如果我们有两类数据(猫和狗的图片),SVM会试图找到一条“最佳分界线”,以便区分猫和狗。
简单来说,支持向量机的目标是找到一条(或多维空间中的一个超平面),能够将不同类别的数据分开,并且这条分界线具有“最大的安全边界”(margin)。
2. 支持向量机的核心概念
要理解支持向量机,我们需要抓住以下几个核心概念:
2.1 超平面(Hyperplane)
在二维空间中,超平面就是一条直线;在三维空间中,超平面是一块平面;而在更高维度中,它是一个更复杂的几何对象。超平面是数据分类的关键,它将不同类别的数据分隔开来。
例如,假设我们有一组二维数据点(x, y),超平面可以表示为:
w1x+w2y+b=0
这里的 w1、w2 和 b 是需要优化的参数。
2.2 间隔(Margin)
支持向量机的目标是找到一个“最大间隔”的超平面。所谓间隔,就是超平面到最近数据点的距离。SVM会试图将这个距离尽可能拉大。为什么要这么做?因为间隔越大,模型的“信心”越足,对新数据的预测更可靠。
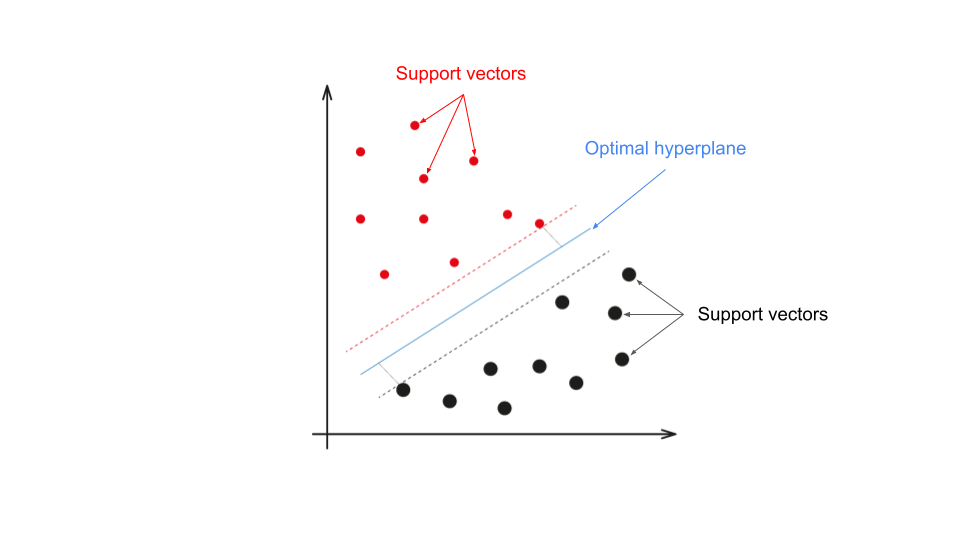
2.3 支持向量(Support Vectors)
并不是所有数据点都对超平面的位置有影响。那些离超平面最近、对模型分类结果有直接影响的数据点,被称为支持向量。这些点是SVM模型学习的关键。
3. 支持向量机是如何工作的?
3.1 线性可分的情况
如果数据可以用一条直线(或一个平面)分开,SVM会在所有可能的分界线中,找到一个能让间隔最大的那条。这就是所谓的“最大间隔分类器”。
假设我们有两类数据,分别标记为+1和-1,支持向量机会优化一个公式:
maximize ∥w∥1 subject to constraints
约束条件是数据点被正确分类,并且距离超平面的间隔大于等于1。
3.2 数据线性不可分的情况
如果数据不能用一条直线分开怎么办?比如,一些数据混杂在一起,SVM会引入两种策略:
- 软间隔(Soft Margin)
SVM允许部分数据点“越界”或“出错”。通过引入一个“惩罚项”来平衡间隔大小和分类错误。 - 核函数(Kernel Function)
如果在原始空间无法分开数据,SVM会利用核函数将数据映射到更高维度。在这个高维空间里,数据可能变得线性可分。
一个常用的比喻是:假设我们在平地上看一个圆圈里的数据,两类数据混在一起很难分开。但如果将其投影到三维空间(比如一个碗的形状),数据就可以轻松用一个平面分隔。这种“映射”的过程就是核函数的作用。
常见的核函数包括:
- 线性核(Linear Kernel)
- 多项式核(Polynomial Kernel)
- 高斯核(Gaussian Kernel)或RBF核
4. 支持向量机的优势和局限
4.1 优势
- 高效性
在小样本数据中,SVM表现极为优秀,特别适合高维数据。 - 强泛化能力
最大间隔的设计让SVM在处理新数据时,具有更好的预测能力。 - 灵活性
通过核函数,SVM可以处理复杂的非线性问题。
4.2 局限性
- 计算复杂度高
SVM在处理大型数据集时,计算效率较低。 - 对参数敏感
核函数和惩罚项的选择对模型性能影响很大,需要经验和调试。 - 难以解释
对于复杂核函数的模型,结果难以直观解释。
5. 支持向量机的应用场景
支持向量机在许多领域都有广泛应用,例如:
- 文本分类
如垃圾邮件检测、情感分析等。 - 图像识别
支持向量机常用于手写数字识别、人脸检测等任务。 - 基因分类
SVM在医疗领域也有应用,如基因数据的分类和疾病预测。 - 金融分析
SVM可用于信用评分、股票价格预测等场景。
6. 结语
支持向量机作为一种经典的机器学习算法,虽然随着深度学习的兴起,它在某些任务中不再占据主导地位,但它仍然是一种高效、可靠的工具,特别是在小数据集和高维问题上。如果你想深入研究分类问题,支持向量机是一个不可或缺的知识点。