逻辑回归是一种非常常用的机器学习方法,尽管名字里有“回归”二字,但它其实是一种分类模型,用来解决“这个东西属于A类还是B类?”的问题。接下来,我们用日常生活中的例子,一步步拆解逻辑回归是如何工作的,并用通俗的语言解释它背后的原理。
1. 问题背景:如何做出分类决策?
假设你是一个水果商,你需要快速判断一个水果是“苹果”还是“橙子”。你会观察水果的特征,比如:
- 颜色(红色倾向苹果,橙色倾向橙子)
- 形状(圆圆的可能是橙子,略扁是苹果)
- 重量(苹果一般比橙子轻一点)
如果你有大量的水果历史数据,比如某些红色、扁圆且重120克的是苹果,而某些橙色、圆且重150克的是橙子,那么你就可以用这些数据训练你的“大脑”,建立一个规则:只要给我一颗水果,我就能通过这些特征推测出它的类别。
逻辑回归就是一种工具,帮助我们用数学方式表达这种分类规则。
2. 逻辑回归的核心思想:划分世界
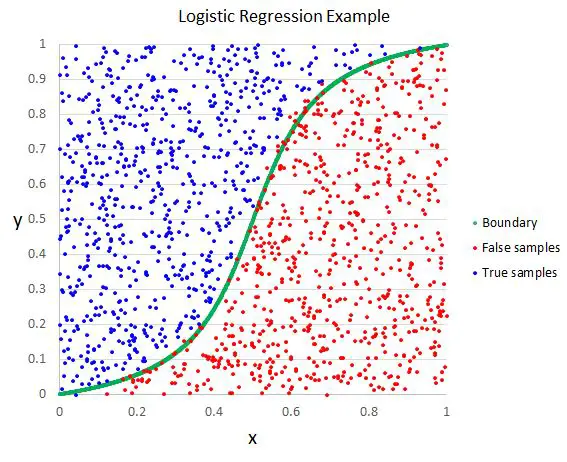
逻辑回归的核心任务是画一条“分界线”。这条分界线会将不同的类别(比如苹果和橙子)分开,并且能够根据新来的数据判断它落在哪一边。
假设我们用颜色和重量这两个特征来分类水果,可以把这些特征画在一张二维平面图上:
- 横轴表示水果的颜色(红色到橙色用数值0到1表示)
- 纵轴表示重量
每个水果都会对应一个点。如果我们发现苹果的数据点大多分布在左下角,而橙子的大多分布在右上角,那么一条对角线就可以大致将它们分开。这条对角线就是逻辑回归在做的事情。
3. 数学背后:逻辑回归如何画“分界线”?
逻辑回归实际上做了两件事:
- 找到一个公式:用来计算一个水果是苹果的可能性。
- 定义一个决策规则:如果可能性超过50%,就判定是苹果,否则是橙子。
公式的核心是一个叫“Sigmoid函数”的工具,它的形状像个“S”,可以把任意的数字压缩到0到1之间。通俗理解:
- 0表示完全不可能,比如“100%是橙子”。
- 1表示完全确定,比如“100%是苹果”。
- 介于0和1之间的数字(比如0.7)表示“有70%的可能性是苹果”。
(1)线性公式:建立“打分”机制
首先,逻辑回归会用一个线性公式给水果打分,比如: 分数=w1×颜色+w2×重量+b 这里的 w1、w2 是逻辑回归需要学习的“权重”,代表颜色和重量在判断类别时的重要性,b 是偏置项,可以简单理解为微调打分的基础值。
举个例子:
- 如果颜色的权重 w1 很大,说明颜色在分类中很重要;
- 如果重量的权重 w2 较小,说明重量的影响比较弱。
(2)Sigmoid函数:将分数变成概率
接下来,把这个分数丢进Sigmoid函数,公式是: P=1+e−分数1
如果分数很大,Sigmoid会输出接近1的值,表示可能性很高;如果分数很小,输出接近0,表示可能性很低。
比如:
- 分数是10,概率接近1(“这绝对是苹果”)。
- 分数是-10,概率接近0(“这绝对是橙子”)。
- 分数是0,概率是0.5(“有点难判断,但两者可能性相同”)。
4. 模型是如何“学习”的?
逻辑回归的学习过程,实际上是在寻找最合适的 w1、w2 和 b,让模型的预测尽可能接近真实答案。这个过程叫做“优化”,主要分为以下几步:
(1)定义损失函数
损失函数是用来衡量模型“预测错误”的程度。逻辑回归用的是“对数损失函数”,它会根据预测概率和实际答案之间的差距计算一个误差值。简单来说:
- 如果预测正确(比如模型预测70%是苹果,而真实标签也是苹果),损失会很小。
- 如果预测错误(比如模型预测90%是橙子,而真实是苹果),损失会很大。
(2)调整权重和偏置
为了让损失越来越小,逻辑回归会用一种叫“梯度下降”的方法来更新权重和偏置。这就好像一个人在迷雾中爬山,虽然看不清全貌,但可以通过“当前的坡度”判断是往上走还是往下走,从而逐步接近最高点。
通过反复调整权重和偏置,模型最终会找到一组最优的参数,让预测结果尽可能准确。
5. 优点和局限性
优点:
- 简单易用:逻辑回归的数学公式简单,计算效率高,很适合入门。
- 解释性强:权重值可以告诉我们每个特征的重要性。
- 适用广泛:不仅可以解决二分类问题,还可以扩展到多分类(叫做Softmax回归)。
局限性:
- 假设太简单:逻辑回归假设数据是线性可分的,但实际中很多问题的分界线并不是一条直线。
- 对特征工程要求高:需要手动提取有效特征,否则效果不好。
- 容易过拟合:如果数据噪声大,逻辑回归可能会学到错误的规律。
6. 总结:逻辑回归是一种简单又强大的分类工具
逻辑回归就像一个聪明的水果商,通过学习历史数据找到水果分类的“分界线”。它先用线性公式打分,再用Sigmoid函数把分数转化为概率,最后根据概率决定类别。
虽然逻辑回归的能力有限,但它简单、高效,是机器学习中非常重要的基础模型。如果我们理解了逻辑回归的工作原理,就能更好地掌握其他复杂的机器学习方法,因为很多模型的核心思想都是从这里扩展出来的。