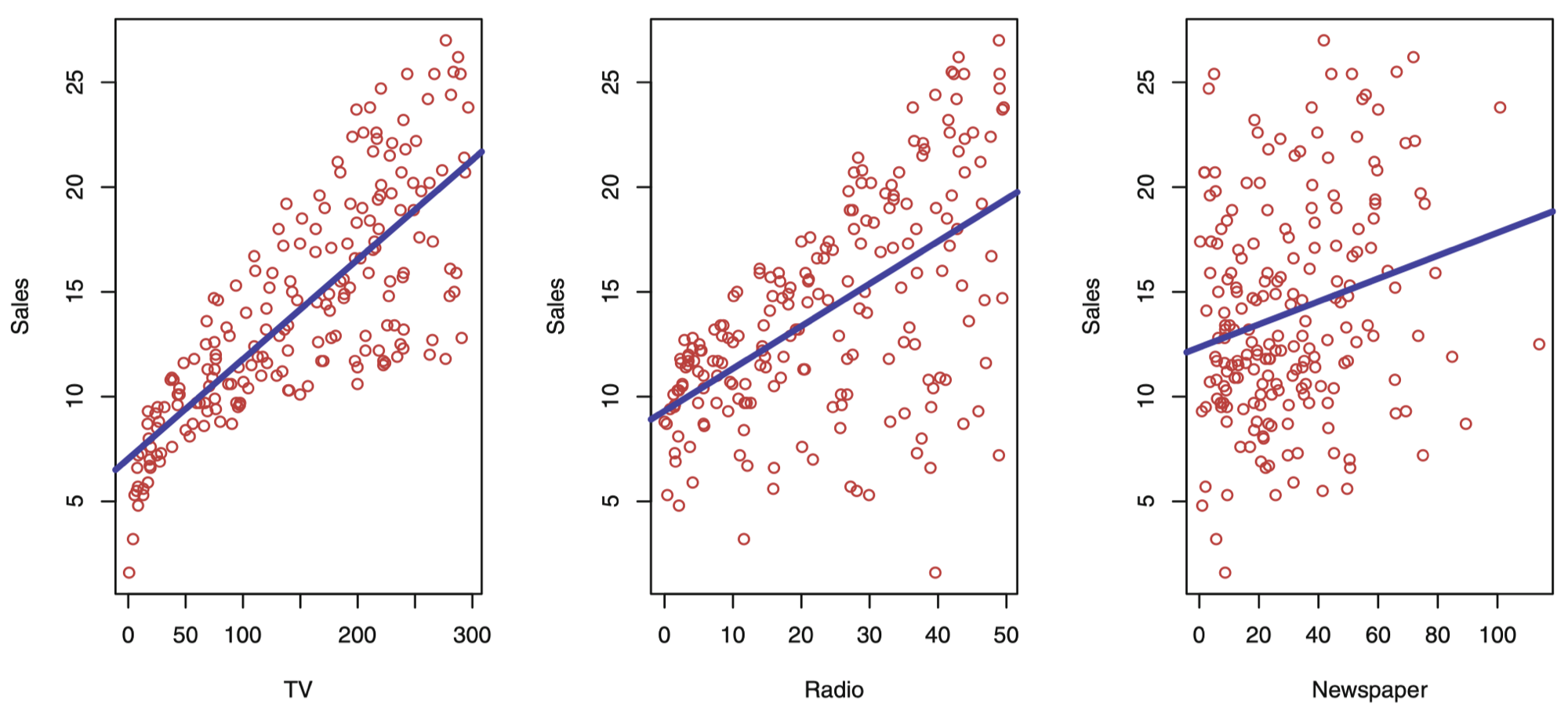
如果你是一名学生、研究员,或者对数据感兴趣,你可能会听过“线性回归”这个词。尽管听起来有些“数学味”,但其实它的核心思想很简单:用一条直线去解释和预测数据。
什么是线性回归?
我们日常生活中经常会发现一种规律:一件事情的变化可能和另一件事情的变化有关。比如:
- 家里的电费可能和用电量有关;
- 一家餐厅的收入可能和当天的顾客数量有关;
- 一个学生的考试成绩可能和复习的时间有关。
线性回归的目标就是找出这些规律,并用一种数学方式表达出来。它尝试用一条直线,来描述两个(或更多)变量之间的关系。
直线的数学公式
大家可能还记得初中学过的直线方程:y=mx+b
这就是线性回归的核心公式!在这里:
- y 是我们想要预测的结果(比如电费、收入、成绩)。
- x 是我们用来预测的东西(比如用电量、顾客数量、复习时间)。
- m 是斜率,表示 y 随着 x 增加或减少的速度。
- b 是截距,表示当 x=0 时, y 的值。
举个例子: 假如我们发现电费的公式是 y=2x+10,那么这意味着:
- 每用1度电(x),电费 y 会增加2元。
- 即使用电量是0(x=0),电费还是有10元(可能是固定费用)。
为什么要用线性回归?
线性回归的最大优点是简单且实用。它帮助我们:
- 解释关系:找到变量之间的关联(比如多复习1小时能提高多少分)。
- 预测未来:根据现有的数据预测未知的结果(比如明天的顾客数量可能带来多少收入)。
- 优化决策:帮助我们根据数据做出更明智的选择(比如如何控制电费支出)。
如何找到“最好”的直线?
我们需要找到一条最能贴合数据的直线。这个过程就是“训练”线性回归模型。
假设有一组数据点(例如一组散点图),我们要画一条直线。不同的直线可能会离这些点有远有近。于是,问题变成了:
我们该如何定义“最接近”的直线?
答案是:最小化误差。
误差就是每个数据点和直线之间的距离(可以理解为“偏差”)。我们希望这些误差的平方和(称为“损失函数”)越小越好。
计算误差的方法如下:
- 对每个数据点,算出它的实际值(真实 y)和预测值(直线给出的 y)的差距。
- 把这些差距平方后加起来。
- 找到一条直线,使得总误差最小。
这种方法叫“最小二乘法”,它是线性回归背后的数学基石。
线性回归的两个“版本”
1. 简单线性回归
这是最基础的形式,只有一个 x 和一个 y。
比如:研究用电量(x)和电费(y)的关系。
2. 多元线性回归
有时候一个结果可能受到多个因素的影响。比如房价可能取决于:
- 房子的面积(x1);
- 房子的地段(x2);
- 房子的装修情况(x3)。
这时,线性回归的公式就变成了:y=m1x1+m2x2+m3x3+b
它仍然是“线性”的,只是变复杂了。
实际应用中的线性回归
- 经济学:预测股票价格、分析市场趋势。
- 医学:研究药物剂量与疗效之间的关系。
- 商业:优化广告支出,预测销量。
- 日常生活:分析健身时间对体重变化的影响。
比如,你是一个游戏开发团队(比如 Now Game Studio),想知道广告投放和游戏下载量的关系。通过线性回归,你可以分析出:每增加100元广告支出,大约能增加多少玩家。
线性回归的局限性
尽管线性回归很强大,但它也有一些限制:
- 只适用于线性关系:如果数据之间的关系是弯曲的,直线就无法很好地描述。
- 对异常值敏感:数据中几个“特别大”或“特别小”的值可能会严重影响结果。
- 忽略复杂的交互关系:现实世界中,变量之间的关系可能很复杂,而线性回归只能处理简单的线性模式。
总结
线性回归是一个强大且简单的工具,它通过一条直线帮助我们解释和预测数据。在它的背后,有清晰的数学逻辑,但在实际应用中,我们更关注它的实用性。无论是学生、科研工作者,还是商业决策者,理解并使用线性回归,都是迈向数据分析世界的重要一步。