类比理解
什么是KL散度?
KL散度,全名是Kullback-Leibler散度,有时也被称为相对熵(Relative Entropy)。听起来名字很复杂,但本质上它的功能很简单:用来衡量两个概率分布之间的“距离”。注意,这种“距离”不是几何意义上的,而是统计意义上的。它用来回答这样一个问题:如果我们用一个分布 Q 来近似另一个分布 P,那么我们会损失多少信息?
类比理解
假设你是一名侦探,你需要判断某个嫌疑人是否有罪。你有两套线索,一个是真实的线索 P,另一个是朋友给的“可能不准确”的线索 Q。KL散度就是用来衡量这两套线索的差别有多大。如果 Q 和 P 差别很小,那么你可以比较放心地使用 Q;但如果差别很大,那么 Q 很可能会误导你。
KL散度的数学公式是这样的:DKL(P∥Q)=x∑P(x)logQ(x)P(x)
或者在连续分布的情况下:DKL(P∥Q)=∫P(x)logQ(x)P(x)dx
这里:
- P(x) 是真实分布中某个事件 x 发生的概率;
- Q(x) 是我们假设分布中该事件发生的概率;
- 公式的核心思想是计算 P 和 Q 在每个事件上的差别,然后加总起来。
直观解释公式
- 分母 Q(x):表示你用的“假设”分布的概率。
- 分子 P(x):表示真实的概率。
- 对数函数 logQ(x)P(x):用来衡量每个事件在 P 和 Q 中的“相对差距”。
比如,P(x) 是 0.8,而 Q(x) 是 0.1,那么对数值会很大,因为 Q 明显偏离了 P。
反之,如果 P(x)=Q(x),那么对数值为 0,表示这个事件没有信息损失。 - 加权平均:把所有事件的对数值乘以 P(x) 后加起来,得到总体的“偏差量”。
特性
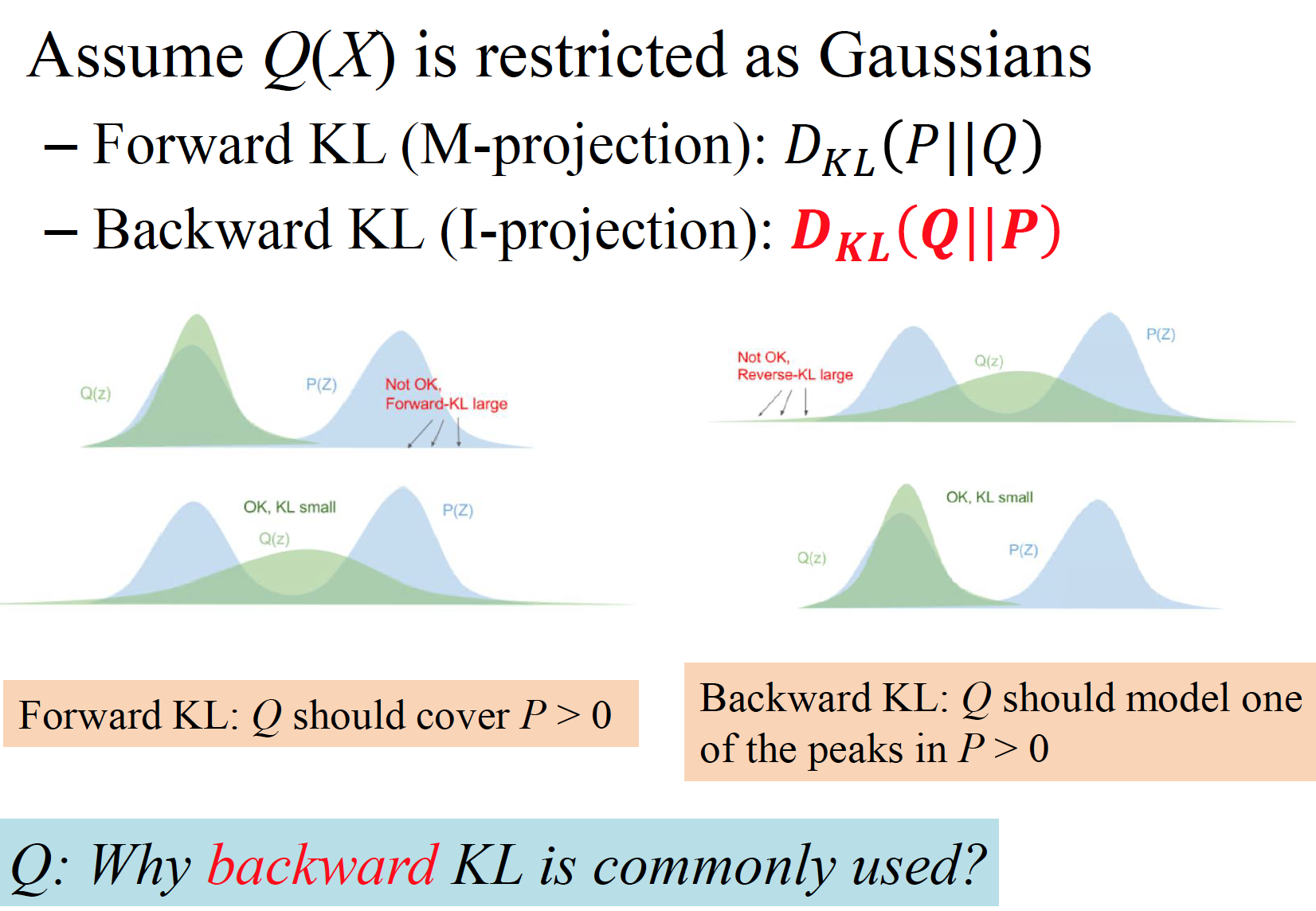
- 非对称性:KL散度对 P 和 Q 的顺序敏感,也就是说 DKL(P∥Q)=DKL(Q∥P)。它衡量的是“用 Q 去近似 P 时的误差”,而不是反过来。
- 非负性:KL散度总是大于等于零,且只有在 P=Q 时等于零。
KL散度与人工智能的关系
在人工智能中,尤其是机器学习和深度学习领域,KL散度被广泛应用于优化、分布拟合和模型评估。以下是一些重要的应用场景:
1. 概率分布匹配
在机器学习中,我们经常需要让模型学习一个目标分布。比如:
- 在自然语言处理(NLP)中,语言模型会尝试预测下一个单词出现的概率分布;
- 在生成式模型(如生成对抗网络、变分自动编码器)中,目标是让生成的分布 Q尽可能接近训练数据的真实分布 P。
通过最小化 KL 散度,可以让模型生成的分布逐渐逼近目标分布,从而提高生成质量。
2. 最大似然估计(MLE)
最大似然估计是机器学习模型训练的核心思想,而 KL散度是它的理论基础。MLE可以看作是最小化真实分布 P 和模型分布 Q 的 KL散度。
举个例子:
- 假如我们有一堆猫狗的图片,真实概率分布 P 是“70% 是猫,30% 是狗”;
- 我们的模型 Q 开始时可能认为“50% 是猫,50% 是狗”;
- 通过最小化 KL散度,我们可以调整模型的参数,让 Q 更接近 P。
3. 变分推断(Variational Inference)
在贝叶斯统计和深度学习中,变分推断是一种用来近似复杂分布的技术。这里的核心思想是用一个简单的分布 Q 来近似真实的后验分布 P。KL散度被用来衡量 Q 和 P 的差距,并指导优化过程。
例如,在变分自动编码器(VAE)中,我们的目标是同时最大化数据的重构能力和最小化 KL散度,使得隐变量的分布更合理。
4. 信息论中的解释
KL散度和信息论的关系也非常紧密。它被认为是信息损失的量化方式。如果我们假设 Q 是真实分布,而它实际上是 P,那么在编码数据时会造成多大的冗余?这种信息论视角为深度学习中的一些损失函数(如交叉熵损失)提供了理论支持。
5. 强化学习
在强化学习中,KL散度被用来控制策略更新的范围。例如,在策略梯度算法(如PPO,Proximal Policy Optimization)中,KL散度被用作一种正则化项,确保新策略不会偏离旧策略太远,从而保证训练的稳定性。
KL散度的实际案例
案例 1:文本生成中的分布匹配
假设你在训练一个语言模型,让它生成像人类一样的句子。真实分布 P 是从一本书中统计得到的单词概率,比如“the”的概率是 10%,“apple”的概率是 2%。你的模型刚开始时可能会认为“the”的概率是 20%,“apple”的概率是 5%。通过最小化 KL散度,你可以让模型逐渐学会更符合书本语言风格的单词分布。
案例 2:变分自动编码器(VAE)
在VAE中,KL散度用于约束隐变量的分布 Q 逼近标准正态分布 P。如果没有这个约束,生成的图像可能会质量较差,且隐空间的表示会混乱。通过 KL 散度,VAE 能学到一种连续的隐空间表示,从而生成逼真的图片。
总结
KL散度是一种非常重要的数学工具,在机器学习和人工智能中有广泛应用。它的核心思想是衡量两个分布之间的差异,为优化模型、匹配分布和控制信息损失提供了一种有效的方式。
无论是训练语言模型、图像生成,还是强化学习,KL散度始终扮演着不可或缺的角色。对KL散度的理解,能够帮助我们更深入地掌握人工智能技术的本质,提高算法设计和优化能力。