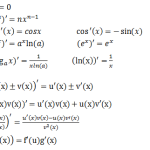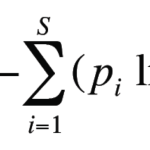微积分与梯度下降:人工智能的幕后推手
引言
支撑人工智能这些技术背后的核心工具之一——梯度下降(Gradient Descent),却源自数学中的微积分。本文将以通俗的语言解读梯度下降的原理,并说明它在人工智能中的关键作用。
什么是梯度下降?
1. 从日常生活入手:寻找最低点
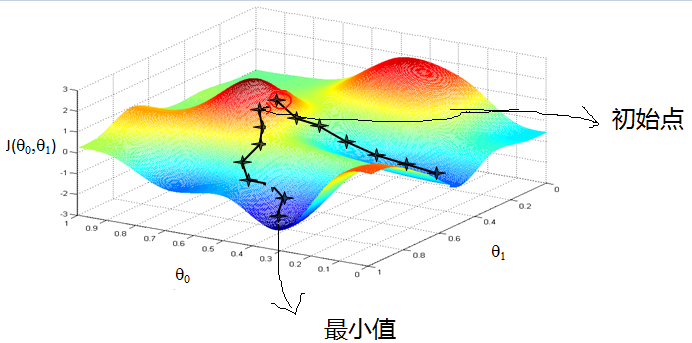
想象一下,你在一个大雾弥漫的山谷中漫步,周围的能见度极低,你看不到远处的地形。但你有一个目标:找到山谷的最低点。为了达到目标,你可以采用一个简单的策略——观察脚下地面的倾斜方向(斜坡的方向),然后沿着向下的方向迈步,重复这个过程直到没有更低的地方。
这个过程就是梯度下降的一个形象化描述。它的核心思想是,通过不断调整自己的位置来逐步接近最低点。
2. 梯度的意义
在数学上,梯度是一个向量,它描述了某个函数在某一点的变化率和方向。对于二维平面来说,梯度可以理解为“斜坡的方向”;而对于更高维度的情况,比如多维空间中的人工智能模型,梯度描述了某个点的“最陡上升方向”。梯度下降所做的,就是沿着梯度的反方向逐步移动。
微积分的作用:梯度是怎么来的?
1. 函数和导数
微积分的基本问题之一是求函数的变化率。导数(上文所讲)是描述这种变化率的工具。例如,对于一个简单的函数 y=x2,它的导数 y′=2x 告诉我们在某一点上函数的变化快慢和方向。
当我们把导数扩展到多维函数时,就得到了“梯度”。在一个复杂的人工智能模型中,目标函数通常有很多个变量,比如模型的参数权重。微积分帮助我们计算每个变量对目标函数的影响,从而得到梯度。
2. 梯度下降公式
梯度下降的更新公式非常简单:θnew=θold−η⋅∇f(θ)
- θ 是模型的参数;
- η 是学习率,决定了每一步的步伐大小;
- ∇f(θ) 是目标函数的梯度。
每一步迭代,我们都使用梯度信息调整参数,使目标函数逐步变小。
梯度下降与人工智能的关系
1. 深度学习中的优化问题
人工智能的核心任务是“让模型学会某种能力”,比如识别图片中的猫或狗。为了让模型学会,我们需要一个目标函数(通常叫“损失函数”),它衡量模型的表现。比如,如果模型的预测结果和真实答案差距很大,损失函数的值就很高;如果预测准确,损失函数的值就很低。
梯度下降的任务就是找到让损失函数最小化的参数配置。这就像是找到山谷的最低点,让模型的误差尽可能小。
2. 深度学习中的复杂性
人工智能中的深度学习模型通常包含数百万甚至数十亿个参数。梯度下降的优点是,它不需要在一开始就知道整个“山谷”的形状,而是通过局部的梯度信息逐步调整模型参数,这使得优化问题在高维空间中变得可行。
3. 梯度下降的改进
由于实际问题的复杂性,单纯的梯度下降在很多情况下可能不够高效。因此,科学家们发明了许多改进版本,例如:
- 随机梯度下降(SGD):在每次更新时只使用一部分数据来计算梯度,提高计算效率;
- 动量法(Momentum):在更新时加入历史梯度的动量,避免陷入局部最小值;
- Adam优化器:对梯度的更新动态调整,适应不同方向的变化速率。
梯度下降如何改变人工智能?
1. 更快的模型训练
梯度下降和它的改进算法使得深度学习模型的训练变得快速而高效。例如,现代的图像识别模型可以在短时间内处理海量数据,这得益于优化算法的进步。
2. 自适应学习
梯度下降允许模型自动调整自己的参数,而无需人为干预。这种“自动化”的能力让人工智能在面对复杂问题时更加灵活和强大。
3. 从理论到应用
梯度下降已经成为人工智能领域的基石。从语音识别到自动驾驶,从机器翻译到医疗诊断,梯度下降帮助科学家将复杂的数学理论转化为改变世界的技术。
一个通俗的例子:梯度下降如何学习画猫?
假设你正在训练一个人工智能模型,让它能够识别猫的图片。模型一开始是“懵的”,它可能会随便猜测“这是一条狗”。损失函数在这个时候会告诉模型:“猜错了,差得远呢!”然后,模型通过梯度下降调整自己的参数,让下次的猜测更接近真实答案。
这就像是一个孩子学习画画。一开始画得很糟糕,但经过不断的调整和练习(类似于梯度下降的多次迭代),最终画出了一只像模像样的猫。
结语
梯度下降,是将抽象的数学微积分与现实应用相结合的桥梁。它不仅是一个简单的优化工具,更是人工智能技术发展的核心引擎。无论是机器学习算法还是深度学习模型,梯度下降都在不断推动着技术的前进,让人工智能从实验室走向生活,改变世界。