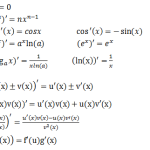微积分中的导数与人工智能的关系:一个通俗的解释
在2.3我们将一起学习微积分在人工智能领域当中的应用
那么第一课,我们先了解导数
引言:为什么要谈导数和人工智能?
在数学的世界里,导数是一个非常核心的概念,它描述了一个量如何随另一个量变化。在日常生活中,导数可以帮助我们理解很多动态现象,比如车的速度(位置的变化率)或者股票的涨跌幅(价格的变化率)。与此同时,在人工智能特别是机器学习中,导数同样扮演着重要角色,它帮助我们优化模型、提升性能,让AI变得更加聪明。
这篇文章会用通俗的语言来解释导数是什么,以及它是如何成为人工智能背后的重要工具的。
什么是导数?
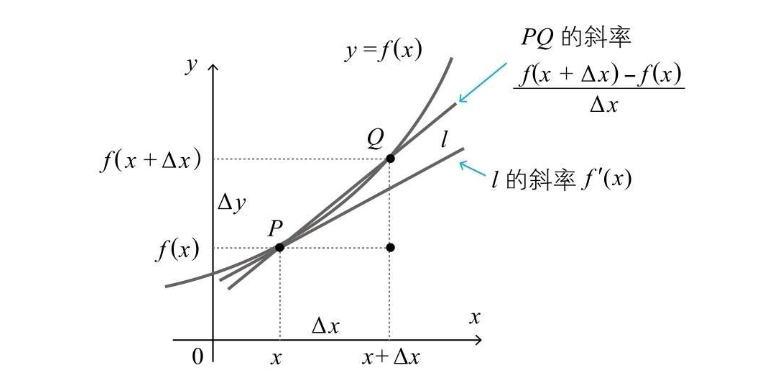
先从一个简单的例子开始:假设你在一条笔直的道路上开车,你的车速表显示“50公里/小时”。这是什么意思呢?简单来说,车速表告诉你“如果你以这个速度继续行驶一小时,你会前进50公里”。这就是一个瞬时速度的概念,而导数正是用来描述这种瞬时变化率的数学工具。
一个更贴近生活的比喻:
- 想象你爬一座山,山的高度随着你前进的距离变化。导数就像一个实时告诉你山坡有多陡的仪器。如果导数为正,说明你在上坡;如果为负,说明你在下坡;如果导数是零,那你正站在一个平坦的地方,可能是山顶或山谷。
在数学上,我们用导数来回答一个核心问题:某个变量改变一点点时,另一个变量会随之改变多少?
人工智能中的导数:机器学习的幕后英雄
机器学习是怎么工作的?
人工智能中的机器学习(比如教会一个程序识别猫狗的图片)本质上是让计算机找到一个“函数”,这个函数能够把输入(比如一张图片的像素数据)和输出(这是一只猫还是一只狗)联系起来。为了找到这个函数,我们通常会定义一个“损失函数”,它用来衡量模型预测的结果和真实答案之间的差距。
导数在优化中的作用
优化问题的核心目标是“让损失函数的值最小化”,也就是让模型的预测越来越准确。这里,导数发挥了至关重要的作用。我们可以用一个简单的比喻来理解这一过程:
- 假设损失函数是一个山坡,而你是一位登山者,你的目标是找到山谷(最低点)。
- 导数就像指南针,它告诉你目前坡的方向和陡峭程度,你应该朝哪个方向迈出下一步。
- 如果导数很大,说明山坡很陡,你需要小心地调整步伐;如果导数很小,说明山坡变得平缓,你已经离山谷很近了。
这种“沿着导数指引的方向前进”的方法在机器学习中叫做梯度下降,它是优化算法的核心。
导数和深度学习:从简单到复杂
在深度学习中,模型通常是由多个“层”组成的,每一层都对数据进行复杂的变换。比如,一个图像分类模型可能由几十层甚至上百层组成,每一层都有数百万甚至更多的参数。
为什么深度学习需要导数?
假设我们想调整这些参数,让模型的表现更好。问题是,每个参数对最终结果的影响都不同,直接猜测是不现实的。这里,导数帮助我们逐一分析每个参数的“贡献”,告诉我们每个参数应该如何调整。这种过程叫做误差反向传播(Backpropagation),它依赖于链式法则——一个数学公式,用来计算多层函数的导数。
一个通俗的总结
从爬山的坡度到AI模型的优化,导数帮助我们理解“变化”这件事。对于人工智能来说,导数不仅是一种数学工具,更是一种语言,它告诉我们如何改进模型,让它更好地预测、更聪明地学习。
导数与未来的人工智能
展望未来,随着人工智能模型的复杂性不断提高,如何有效地计算导数以及利用导数优化模型将变得更加重要。例如,在自动驾驶中,导数帮助车辆做出快速决策;在医疗诊断中,它优化模型以提高疾病预测的准确性。
更深层次地看,导数的概念也在引导着我们对智能本身的理解。通过研究“变化”和“调整”,我们不仅能够打造更聪明的机器,还可以更好地理解人类智能的动态本质。
希望这篇文章用直观的方式解答了导数和人工智能之间的关系。无论是数学还是AI,导数的核心理念——“变化率”——都是帮助我们探索未知、优化未来的关键。