2.1.4 线性变换和向量空间

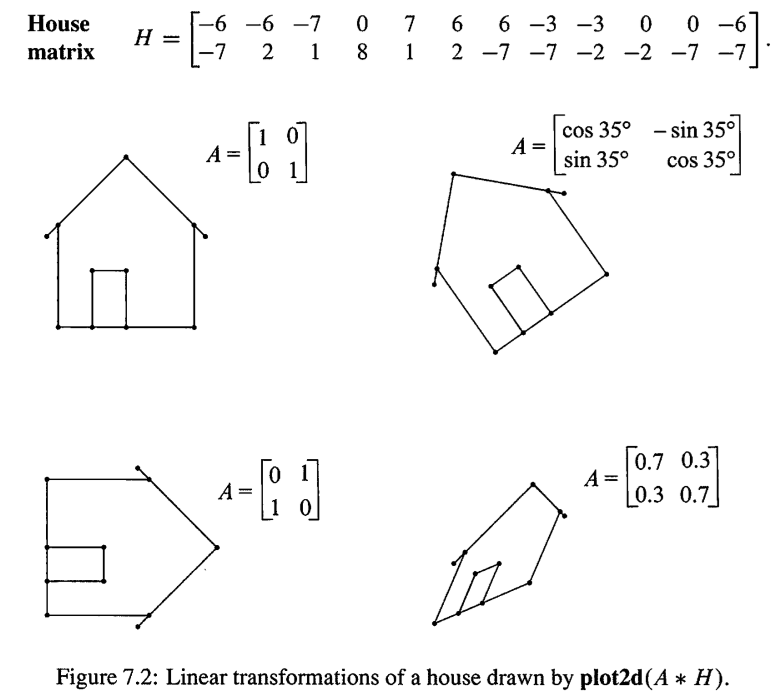
关于线性代数关于AI的关系就讲完了，既然提到了线性代数，就额外讲一下剩下两个重要组成，线性变换和向量空间

什么是线性变换？

线性变换是数学中的一个概念，简单来说，它是一种规则，把一个向量变成另一个向量，同时满足以下两个特性：

1. 加法保持性：
   线性变换对向量的加法是保持的。
   如果 TT 是一个线性变换，那么对任意向量 uu 和 vv，T(u+v)=T(u)+T(v)T(u+v)=T(u)+T(v)
2. 数乘保持性：
   线性变换对向量的数乘是保持的。
   如果 TT 是一个线性变换，那么对任意向量 vv 和标量 cc，T(c⋅v)=c⋅T(v)T(c⋅v)=c⋅T(v)

通俗点说，线性变换是一种非常“规矩”的变换，它不会让向量的基本关系乱套。例如，把一张方格纸变形后，如果线条仍然是直线且交点仍然是格点，这个变换就是线性的。

例子：

• 把一个向量拉长（伸缩）或旋转是线性变换。
• 把一个向量弯曲或剪切后再拼接，就不是线性变换。

---

什么是向量空间？

向量空间是一个数学结构，它定义了“向量”可以如何组合和运算。通俗来说，向量空间就像一个“操场”，里面的规则规定了可以怎么玩，比如加法、数乘等。

向量空间的特点：

1. 加法闭合：两个向量相加，结果仍然是向量空间中的一个向量。
2. 数乘闭合：一个向量乘以标量，结果仍然在向量空间内。
3. 零向量：向量空间里必须有一个“零向量”，加上它等于原向量。
4. 分配律与结合律：运算必须满足加法与数乘的基本规则。

例子：

• 常见的向量空间包括二维平面上的向量（如 (x,y)(x,y)），三维空间中的向量（如 (x,y,z)(x,y,z)），甚至包括函数（可以看作无限维的向量）。

---

结合在一起理解：

可以把线性变换理解为向量空间内的一种“操作”或“魔法”，它遵守特定的规则，比如把所有向量压缩、旋转或投影到另一个空间。比如：

1. 如果把二维平面上的所有向量都旋转 45∘45∘，这是一个线性变换。
2. 如果把三维空间中的所有向量都投影到一个平面上，也是线性变换。

直观上，向量空间是“玩向量”的地方，而线性变换是“改变向量”的工具。