引言
在人工智能(AI)的世界中,不确定性是常态。无论是图像识别中的模糊边界,还是自然语言处理中的歧义,都充满了随机性和不确定性。而贝叶斯定理,作为概率论中的一个核心概念,为我们提供了一种处理不确定性的有力工具。它不仅是统计学的基础,也是人工智能众多领域的核心算法。贝叶斯定理看起来很数学,但其实它本质上是关于如何更新我们的信念。不管是日常生活还是科学推理,我们都会根据新信息调整对某件事情的判断。贝叶斯定理就是一个数学框架,用来告诉我们应该怎样合理地更新这些信念。
贝叶斯定理是什么?
举个例子:感冒和咳嗽
假设你早上醒来发现自己咳嗽了。你可能会想:
“我是不是感冒了?”
但你也知道,咳嗽不仅仅是感冒的症状,它可能还和过敏、干燥空气、甚至某些疾病(比如肺炎)有关。现在问题来了:
“咳嗽的时候,我得感冒的可能性有多大?”
这就是贝叶斯定理的核心思想:通过观察新证据(咳嗽),重新评估事件的可能性(是否感冒)。
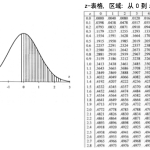
贝叶斯定理描述了如何在新的证据出现时,更新已有的信念。用公式表示为:
P(A|B) = (P(B|A) * P(A)) / P(B)
其中:
P(A|B):在事件B发生的情况下,事件A发生的概率(后验概率)
P(B|A):在事件A发生的情况下,事件B发生的概率(似然度)
P(A):事件A发生的先验概率
P(B):事件B发生的概率(证据)
贝叶斯定理在人工智能中的应用
1. 机器学习
朴素贝叶斯分类器: 将特征假设为相互独立,根据贝叶斯定理计算出样本属于各个类别的后验概率,从而进行分类。
贝叶斯网络: 用有向无环图表示变量之间的概率关系,通过贝叶斯推断进行推理。
贝叶斯优化: 在超参数调优中,通过贝叶斯定理建立概率模型,高效地搜索最优参数。
2. 自然语言处理
语言模型: N-gram模型、主题模型等都基于贝叶斯思想,通过统计词语的共现概率来预测下一个词。
机器翻译: 基于统计的机器翻译模型利用贝叶斯定理来计算翻译结果的概率。
3. 计算机视觉
图像分类: 将图像特征作为证据,利用贝叶斯定理计算图像属于各个类别的概率。
目标检测: 通过贝叶斯网络建模目标与图像区域之间的关系。
4. 强化学习
在强化学习中,智能体需要在不确定的环境中探索和学习。贝叶斯方法可以帮助智能体更好地平衡探索与利用的关系:
贝叶斯强化学习
通过建模环境的不确定性,智能体可以动态调整其行为策略。例如,在多臂老虎机问题中,贝叶斯方法可以利用后验概率更高效地选择拉杆。
模型不确定性建模
在复杂环境中,智能体通常对模型的准确性缺乏信心。贝叶斯方法能够量化这种不确定性,从而优化长期决策。
优势:
处理不确定性: 贝叶斯方法能够量化不确定性,提供概率性的预测结果。
可解释性: 贝叶斯模型的结构清晰,易于解释。
先验知识融入: 可以将先验知识融入模型中,提高模型的性能。
挑战:
计算复杂度高: 特别是对于复杂的模型和大量数据。
先验分布的选择: 先验分布的选择会影响后验分布,需要谨慎选择。
模型假设: 模型假设的合理性会影响模型的性能。
贝叶斯方法的未来发展
贝叶斯深度学习: 将贝叶斯方法与深度学习结合,提高深度学习模型的可解释性。
贝叶斯强化学习: 在不确定环境下进行决策。
贝叶斯因果推理: 从观测数据中发现因果关系。
总结
贝叶斯定理为人工智能提供了强大的概率推理工具。通过将贝叶斯方法与现代机器学习技术相结合,我们可以构建更加鲁棒、可解释、适应性强的智能系统。未来,贝叶斯方法将在人工智能的各个领域发挥更加重要的作用。